Building a Recommender System from Scratch

Step 1: Import Dependencies

We are using pandas.DataFrame to represent our data. We will visualize our data with matplotlib and seaborn.

What is a DataFrame?

• a two-dimensional Pandas data structure
• columns represent features, rows represent items
• analogous to an Excel spreadsheet or SQL table
• documentation can be found here

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

Step 2: Load Data

Let’s download a small version of the MovieLens dataset. See here for zip file url, or directly download here. We’re working with data in ml-latest-small.zip and will need to add the following files to our repository:

• ratings.csv
• movies.csv

Alternatively, you can access the data here:

• https://s3-us-west-2.amazonaws.com/recommender-tutorial/movies.csv
• https://s3-us-west-2.amazonaws.com/recommender-tutorial/ratings.csv

ratings = pd.read_csv('data/ratings.csv')

movies = pd.read_csv('data/movies.csv')

Step 3: Exploratory Data Analysis

n_ratings = len(ratings)
n_movies = ratings['movieId'].nunique()
n_users = ratings['userId'].nunique()

print(f"Number of ratings: {n_ratings}")
print(f"Number of unique movieId's: {n_movies}")
print(f"Number of unique users: {n_users}")
print(f"Average number of ratings per user: {round(n_ratings/n_users, 2)}")
print(f"Average number of ratings per movie: {round(n_ratings/n_movies, 2)}")

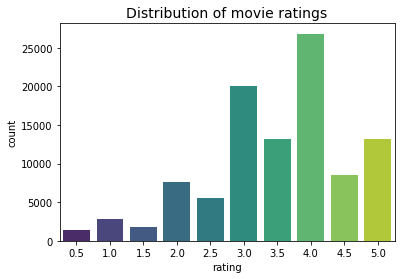
Number of ratings: 100836
Number of unique movieId's: 9724
Number of unique users: 610
Average number of ratings per user: 165.3
Average number of ratings per movie: 10.37

sns.countplot(x="rating", data=ratings, palette="viridis")
plt.title("Distribution of movie ratings", fontsize=14)
plt.show()

print(f"Mean global rating: {round(ratings['rating'].mean(),2)}.")

mean_ratings = ratings.groupby('userId')['rating'].mean()
print(f"Mean rating per user: {round(mean_ratings.mean(),2)}.")

Mean global rating: 3.5.
Mean rating per user: 3.66.

Best vs. Worst Movie

Which movie has the lowest and highest average rating?

mean_ratings = ratings.groupby('movieId')[['rating']].mean()
lowest_rated = mean_ratings['rating'].idxmin()
movies[movies['movieId'] == lowest_rated]

	movieId	title	genres
2689	3604	Gypsy (1962)	Musical

Gypsy has the lowest average rating.

highest_rated = mean_ratings['rating'].idxmax()
movies[movies['movieId'] == highest_rated]

	movieId	title	genres
48	53	Lamerica (1994)	Adventure|Drama

Lamerica may be the “highest” rated movie, but it only has one rating. A better approach for evaluating movie popularity is to do look at the Bayesian average.

Bayesian Average

Bayesian Average is defined as:

\(r_{i} = \frac{C \times m + \Sigma{\text{reviews}}}{C+N}\)

where \(C\) represents our confidence, \(m\) represents our prior, and \(N\) is the total number of reviews for movie \(i\). In this case, our prior will be the average rating across all movies. By defintion, C represents “the typical data set size”. Let’s make \(C\) be the average number of ratings for a given movie.

movie_stats = ratings.groupby('movieId')[['rating']].agg(['count', 'mean'])
movie_stats.columns = movie_stats.columns.droplevel()

C = movie_stats['count'].mean()
m = movie_stats['mean'].mean()

def bayesian_avg(ratings):
    bayesian_avg = (C*m+ratings.sum())/(C+ratings.count())
    return bayesian_avg

bayesian_avg_ratings = ratings.groupby('movieId')['rating'].agg(bayesian_avg).reset_index()
bayesian_avg_ratings.columns = ['movieId', 'bayesian_avg']
movie_stats = movie_stats.merge(bayesian_avg_ratings, on='movieId')

movie_stats = movie_stats.merge(movies[['movieId', 'title']])
movie_stats.sort_values('bayesian_avg', ascending=False).head()

	movieId	count	mean	bayesian_avg	title
277	318	317	4.429022	4.392070	Shawshank Redemption, The (1994)
659	858	192	4.289062	4.236457	Godfather, The (1972)
2224	2959	218	4.272936	4.227052	Fight Club (1999)
224	260	251	4.231076	4.192646	Star Wars: Episode IV - A New Hope (1977)
46	50	204	4.237745	4.190567	Usual Suspects, The (1995)

Using the Bayesian average, we see that Shawshank Redemption, The Godfather, and The Usual Suspects are the most highly rated movies. This result makes much more sense since these movies are critically acclaimed films.

movie_stats.sort_values('bayesian_avg', ascending=True).head()

	movieId	count	mean	bayesian_avg	title
1172	1556	19	1.605263	2.190377	Speed 2: Cruise Control (1997)
2679	3593	19	1.657895	2.224426	Battlefield Earth (2000)
1372	1882	33	1.954545	2.267268	Godzilla (1998)
1144	1499	27	1.925926	2.296800	Anaconda (1997)
1988	2643	16	1.687500	2.306841	Superman IV: The Quest for Peace (1987)

With Bayesian averaging, it looks like Speed 2: Cruise Control, Battlefield Earth, and Godzilla are the worst rated movies. Gypsy isn’t so bad after all.

A Glimpse at Movie Genres

The movies dataset needs to be cleaned in two ways:

• genres is expressed as a string with a pipe | separating each genre. We will manipulate this string into a list, which will make it much easier to analyze.
• title currently has (year) appended at the end. We will extract year from each title string and create a new column for it.

movies['genres'] = movies['genres'].apply(lambda x: x.split("|"))
movies.head()

	movieId	title	genres
0	1	Toy Story (1995)	[Adventure, Animation, Children, Comedy, Fantasy]
1	2	Jumanji (1995)	[Adventure, Children, Fantasy]
2	3	Grumpier Old Men (1995)	[Comedy, Romance]
3	4	Waiting to Exhale (1995)	[Comedy, Drama, Romance]
4	5	Father of the Bride Part II (1995)	[Comedy]

How many movie genres are there?

from collections import Counter

genre_frequency = Counter(g for genres in movies['genres'] for g in genres)

print(f"There are {len(genre_frequency)} genres.")

genre_frequency

There are 20 genres.

Counter({'Adventure': 1263,
         'Animation': 611,
         'Children': 664,
         'Comedy': 3756,
         'Fantasy': 779,
         'Romance': 1596,
         'Drama': 4361,
         'Action': 1828,
         'Crime': 1199,
         'Thriller': 1894,
         'Horror': 978,
         'Mystery': 573,
         'Sci-Fi': 980,
         'War': 382,
         'Musical': 334,
         'Documentary': 440,
         'IMAX': 158,
         'Western': 167,
         'Film-Noir': 87,
         '(no genres listed)': 34})

print("The 5 most common genres: \n", genre_frequency.most_common(5))

The 5 most common genres:
 [('Drama', 4361), ('Comedy', 3756), ('Thriller', 1894), ('Action', 1828), ('Romance', 1596)]

Step 4: Data Pre-processing

We are going to use a technique called colaborative filtering to generate recommendations for users. This technique is based on the premise that similar people like similar things.

The first step is to transform our data into a user-item matrix, also known as a “utility” matrix. In this matrix, rows represent users and columns represent movies. The beauty of collaborative filtering is that it doesn’t require any information about the users or the movies user to generate recommendations.

from IPython.display import Image

Image("imgs/user-movie-matrix.png")

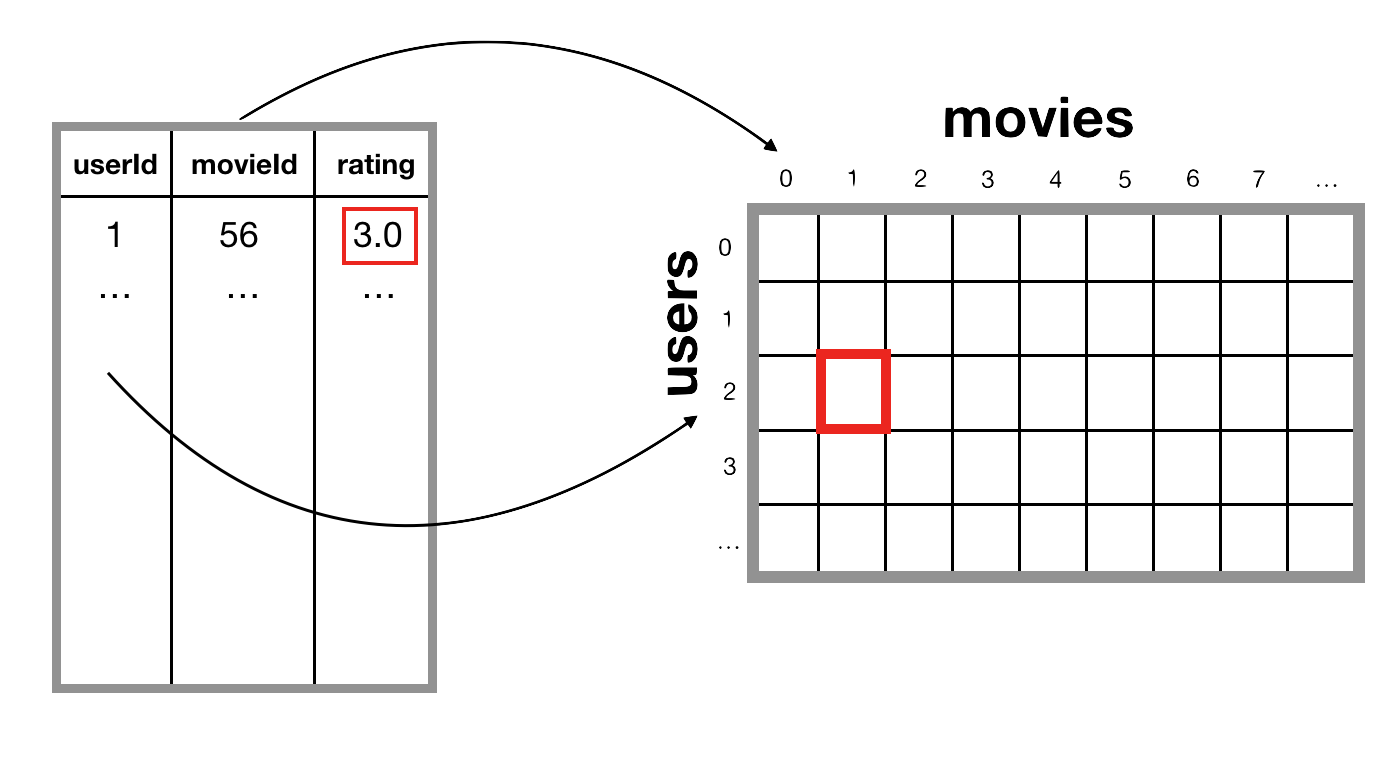
The create_X() function outputs a sparse matrix X with four mapper dictionaries:

• user_mapper: maps user id to user index
• movie_mapper: maps movie id to movie index
• user_inv_mapper: maps user index to user id
• movie_inv_mapper: maps movie index to movie id

We need these dictionaries because they map which row/column of the utility matrix corresponds to which user/movie id.

Our X (user-item) matrix is a scipy.sparse.csr_matrix which stores the data sparsely.

from scipy.sparse import csr_matrix

def create_X(df):
    """
    Generates a sparse matrix from ratings dataframe.

    Args:
        df: pandas dataframe containing 3 columns (userId, movieId, rating)

    Returns:
        X: sparse matrix
        user_mapper: dict that maps user id's to user indices
        user_inv_mapper: dict that maps user indices to user id's
        movie_mapper: dict that maps movie id's to movie indices
        movie_inv_mapper: dict that maps movie indices to movie id's
    """
    M = df['userId'].nunique()
    N = df['movieId'].nunique()

    user_mapper = dict(zip(np.unique(df["userId"]), list(range(M))))
    movie_mapper = dict(zip(np.unique(df["movieId"]), list(range(N))))

    user_inv_mapper = dict(zip(list(range(M)), np.unique(df["userId"])))
    movie_inv_mapper = dict(zip(list(range(N)), np.unique(df["movieId"])))

    user_index = [user_mapper[i] for i in df['userId']]
    item_index = [movie_mapper[i] for i in df['movieId']]

    X = csr_matrix((df["rating"], (user_index,item_index)), shape=(M,N))

    return X, user_mapper, movie_mapper, user_inv_mapper, movie_inv_mapper

X, user_mapper, movie_mapper, user_inv_mapper, movie_inv_mapper = create_X(ratings)

Evaluating sparsity

Here, we calculate sparsity by dividing the number of stored elements by total number of elements. The number of stored (non-empty) elements in our matrix is equivalent to the number of ratings in our dataset.

n_total = X.shape[0]*X.shape[1]
n_ratings = X.nnz
sparsity = n_ratings/n_total
print(f"Matrix sparsity: {round(sparsity*100,2)}%")

Matrix sparsity: 1.7%

csr_matrix.nnz counts the stored values in our sparse matrix. The rest of our cells are empty.

The cold start problem is when there are new users and movies in our matrix that do not have any ratings. In our Movielens dataset, all users and movies have at least one rating but in general, it’s useful to check which users and movies have few interactions.

n_ratings_per_user = X.getnnz(axis=1)

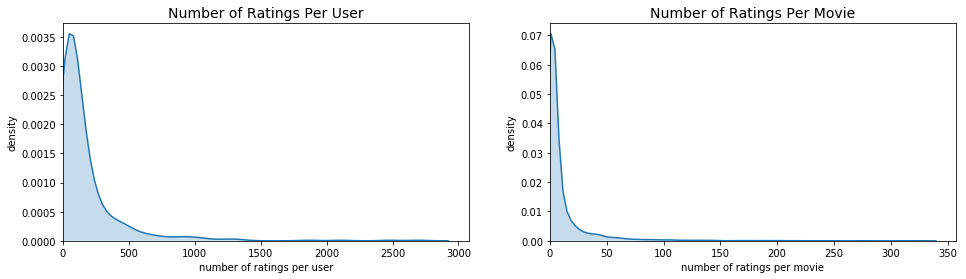
print(f"Most active user rated {n_ratings_per_user.max()} movies.")
print(f"Least active user rated {n_ratings_per_user.min()} movies.")

Most active user rated 2698 movies.
Least active user rated 20 movies.

n_ratings_per_movie = X.getnnz(axis=0)

print(f"Most rated movie has {n_ratings_per_movie.max()} ratings.")
print(f"Least rated movie has {n_ratings_per_movie.min()} ratings.")

Most rated movie has 329 ratings.
Least rated movie has 1 ratings.

plt.figure(figsize=(16,4))
plt.subplot(1,2,1)
sns.kdeplot(n_ratings_per_user, shade=True)
plt.xlim(0)
plt.title("Number of Ratings Per User", fontsize=14)
plt.xlabel("number of ratings per user")
plt.ylabel("density")
plt.subplot(1,2,2)
sns.kdeplot(n_ratings_per_movie, shade=True)
plt.xlim(0)
plt.title("Number of Ratings Per Movie", fontsize=14)
plt.xlabel("number of ratings per movie")
plt.ylabel("density")
plt.show()

Normalizing our data

User-item bias is defined as: \(b_{ui} = \mu + b_{u} + b_{i}\)

We will perform mean normalization by subtracting \(b_{i}\) from each movie’s rating.

sum_ratings_per_movie = X.sum(axis=0)
mean_rating_per_movie = sum_ratings_per_movie/n_ratings_per_movie

Now that we have the mean rating for each movie, we are going to subtract this from our utility matrix. In order to do this, we need to expand our 1D mean_rating_per_movie array into a matrix with the same shape as our utility matrix (n_users, n_movies). Numpy’s tile method is useful for this task.

X_mean_movie = np.tile(mean_rating_per_movie, (X.shape[0],1))

X_mean_movie.shape

(610, 9724)

X_mean_movie is a matrix of shape (n_users, n_movies) in which each column is populated with a given movie’s mean rating.

We can easily normalize our X matrix by subtracting X_mean_movie from original X.

X_norm = X - csr_matrix(X_mean_movie)

As expected, X_norm’s values are different from Xs. Cells that are empty in the original matrix are now replaced with negative values representing the mean rating of a given movie.

print("Original X:", X[0].todense())
print("Normalized X:", X_norm[0].todense())

Original X: [[4. 0. 4. ... 0. 0. 0.]]
Normalized X: [[ 0.07906977 -3.43181818  0.74038462 ... -3.5        -3.5
  -4.        ]]

Step 5: Item-item Recommendations with k-Nearest Neighbors

We are going to find the \(k\) movies that have the most similar user engagement vectors for movie \(i\).

from sklearn.neighbors import NearestNeighbors

def find_similar_movies(movie_id, X, movie_mapper, movie_inv_mapper, k, metric='cosine'):
    """
    Finds k-nearest neighbours for a given movie id.

    Args:
        movie_id: id of the movie of interest
        X: user-item utility matrix
        k: number of similar movies to retrieve
        metric: distance metric for kNN calculations

    Output: returns list of k similar movie ID's
    """
    X = X.T
    neighbour_ids = []

    movie_ind = movie_mapper[movie_id]
    movie_vec = X[movie_ind]
    if isinstance(movie_vec, (np.ndarray)):
        movie_vec = movie_vec.reshape(1,-1)
    # use k+1 since kNN output includes the movieId of interest
    kNN = NearestNeighbors(n_neighbors=k+1, algorithm="brute", metric=metric)
    kNN.fit(X)
    neighbour = kNN.kneighbors(movie_vec, return_distance=False)
    for i in range(0,k):
        n = neighbour.item(i)
        neighbour_ids.append(movie_inv_mapper[n])
    neighbour_ids.pop(0)
    return neighbour_ids

find_similar_movies() takes in a movieId and X matrix, and outputs a list of \(k\) movies that are similar to the movieId of interest.

Let’s see how it works in action. We will first create another mapper that maps movieId to title so that our results are interpretable.

similar_movies = find_similar_movies(1, X_norm, movie_mapper, movie_inv_mapper, k=10)
similar_movies

[3114, 78499, 2054, 788, 2355, 2018, 596, 2078, 673]

find_similar_movies() returns a list of movieId’s that are most similar to your movie of interest. Let’s convert these id’s to titles so that we can interpret our results. To make things easier, we will create a dictionary that maps movieId to title.

movie_titles = dict(zip(movies['movieId'], movies['title']))

movie_id = 1

similar_movies = find_similar_movies(movie_id, X_norm, movie_mapper, movie_inv_mapper, metric='cosine', k=10)
movie_title = movie_titles[movie_id]

print(f"Because you watched {movie_title}:")
for i in similar_movies:
    print(movie_titles[i])

Because you watched Toy Story (1995):
Toy Story 2 (1999)
Toy Story 3 (2010)
Honey, I Shrunk the Kids (1989)
Nutty Professor, The (1996)
Bug's Life, A (1998)
Bambi (1942)
Pinocchio (1940)
Jungle Book, The (1967)
Space Jam (1996)

The results above show the 10 movies that are most similar to Toy Story. Most movies in this list are family movies from the 1990s, which seems pretty reasonable. Note that these recommendations are based solely on user-item ratings. Movie features such as genres are not used in this approach.

You can also play around with the kNN distance metric and see what results you would get if you use “manhattan” or “euclidean” instead of “cosine”.

movie_id = 1

similar_movies = find_similar_movies(movie_id, X_norm, movie_mapper, movie_inv_mapper, metric='euclidean', k=10)
movie_title = movie_titles[movie_id]

print(f"Because you watched {movie_title}:")
for i in similar_movies:
    print(movie_titles[i])

Because you watched Toy Story (1995):
Honey, I Shrunk the Kids (1989)
Nutty Professor, The (1996)
Space Jam (1996)
Mighty Ducks, The (1992)
The Amazing Spider-Man 2 (2014)
Popeye (1980)
Hocus Pocus (1993)
Lost World: Jurassic Park, The (1997)
Snakes on a Plane (2006)

Step 6: Handling the cold-start problem

Collaborative filtering relies solely on user-item interactions within the utility matrix. The issue with this approach is that brand new users or items with no iteractions get excluded from the recommendation system. This is called the cold start problem. Content-based filtering is a way to handle this problem by generating recommendations based on user and item features.

First, we need to convert the genres column into binary features. Each genre will have its own column in the dataframe, and will be populated with 0 or 1.

n_movies = movies['movieId'].nunique()
print(f"There are {n_movies} unique movies in our movies dataset.")

There are 9742 unique movies in our movies dataset.

genres = set(g for G in movies['genres'] for g in G)

for g in genres:
    movies[g] = movies.genres.transform(lambda x: int(g in x))

movie_genres = movies.drop(columns=['movieId', 'title','genres'])

movie_genres.head()

	Action	Film-Noir	Adventure	War	Children	Drama	(no genres listed)	Mystery	Animation	Musical	Horror	Documentary	Western	Romance	Sci-Fi	Fantasy	Crime	Thriller	Comedy	IMAX
0	0	0	1	0	1	0	0	0	1	0	0	0	0	0	0	1	0	0	1	0
1	0	0	1	0	1	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0
2	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	1	0
3	0	0	0	0	0	1	0	0	0	0	0	0	0	1	0	0	0	0	1	0
4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0

from sklearn.metrics.pairwise import cosine_similarity

cosine_sim = cosine_similarity(movie_genres, movie_genres)
print(f"Dimensions of our genres cosine similarity matrix: {cosine_sim.shape}")

Dimensions of our genres cosine similarity matrix: (9742, 9742)

The dimensions of our cosine similarity matrix are \(M \times M\) where \(M\) represents the total number of movies.

def movie_finder(title):
    return movies[movies['title'].str.contains(title)]['title'].tolist()

movie_finder('Toy Story')

['Toy Story (1995)', 'Toy Story 2 (1999)', 'Toy Story 3 (2010)']

movie_idx = dict(zip(movies['title'], list(movies.index)))
title = movie_finder('Toy Story')[0]
n_recommendations = 10

idx = movie_idx[title]
sim_scores = list(enumerate(cosine_sim[idx]))
sim_scores = sorted(sim_scores, key=lambda x: x[1], reverse=True)
sim_scores = sim_scores[1:(n_recommendations+1)]
similar_movies = [i[0] for i in sim_scores]

print(f"Recommendations for {title}:")
movies['title'].iloc[similar_movies]

Recommendations for Toy Story (1995):

1706                                          Antz (1998)
2355                                   Toy Story 2 (1999)
2809       Adventures of Rocky and Bullwinkle, The (2000)
3000                     Emperor's New Groove, The (2000)
3568                                Monsters, Inc. (2001)
6194                                     Wild, The (2006)
6486                               Shrek the Third (2007)
6948                       Tale of Despereaux, The (2008)
7760    Asterix and the Vikings (Astérix et les Viking...
8219                                         Turbo (2013)
Name: title, dtype: object

With this approach, we are assuming that two movies are “similar” if they have similar genres. These “similar movie” recommendations are based solely on the metadata from our movies dataset. Feel free to test out different movies.

Step 7: Dimensionality Reduction with Matrix Factorization (advanced)

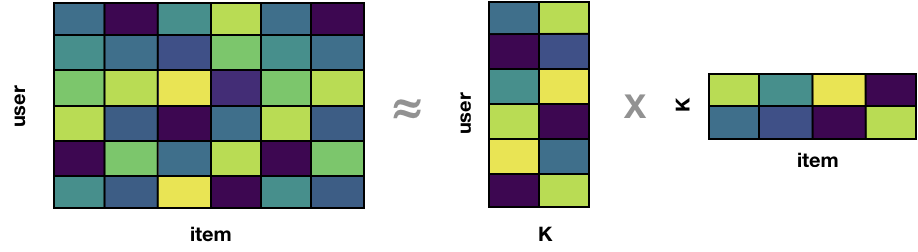
Matrix factorization (MF) is a linear algebra technique that can help us discover latent features underlying the interactions between users and movies. These latent features give a more compact representation of user tastes and item descriptions. MF is particularly useful for very sparse data and can enhance the quality of recommendations. The algorithm works by factorizing the original user-item matrix into two factor matrices:

• user-factor matrix (n_users, k)
• item-factor matrix (k, n_items)

We are reducing the dimensions of our original matrix into “taste” dimensions. We cannot interpret what each latent feature \(k\) represents. However, we could imagine that one latent feature may represent users who like romantic comedies from the 1990s, while another latent feature may represent movies which are independent foreign language films.

\[X_{mn}\approx P_{mk}\times Q_{nk}^T = \hat{X}\]

Image("imgs/matrix-factorization.png")

from sklearn.decomposition import TruncatedSVD

svd = TruncatedSVD(n_components=20, n_iter=10)
Z = svd.fit_transform(X.T)

movie_id = 1
similar_movies = find_similar_movies(movie_id, Z.T, movie_mapper, movie_inv_mapper, metric='cosine', k=10)
movie_title = movie_titles[movie_id]

print(f"Because you watched {movie_title}:")
for i in similar_movies:
    print(movie_titles[i])

Because you watched Toy Story (1995):
Home Alone (1990)
Jurassic Park (1993)
Aladdin (1992)
Willy Wonka & the Chocolate Factory (1971)
Forrest Gump (1994)
Back to the Future (1985)
Groundhog Day (1993)
Star Wars: Episode IV - A New Hope (1977)
Babe (1995)

The results above are the most similar movies to Toy Story using kNN on our “compressed” movie-factor matrix. We reduced the dimensions down to n_components=30. We can think of each component representing a latent feature such as movie genre.

Predicting missing ratings to generate top N recommendations

With matrix factorization, we can also predict missing ratings in our original user-item matrix. We can do this by reconstructing our matrix by getting the inner product of our user-factor matrix and movie-factor matrix. We can use the inverse_transform on our movie-factor matrix Z to get our reconstructed user-item matrix.

new_X = svd.inverse_transform(Z).T

Let’s look at userId=100’s recommendations. In the table below, we can see which movies that have been rated highly:

userId = 100
user_preferences = ratings[(ratings['userId']==userId)&(ratings['rating']>=4)]
user_preferences = user_preferences.merge(movies[['movieId', 'title']])
user_preferences.sort_values('rating', ascending=False).head(10)

	userId	movieId	rating	timestamp	title
97	100	5620	5.0	1100186982	Sweet Home Alabama (2002)
89	100	4041	5.0	1100184235	Officer and a Gentleman, An (1982)
64	100	1958	5.0	1100186258	Terms of Endearment (1983)
45	100	1101	5.0	1100184137	Top Gun (1986)
75	100	2423	5.0	1100186118	Christmas Vacation (National Lampoon's Christm...
1	100	16	4.5	1100185959	Casino (1995)
36	100	919	4.5	1100183748	Wizard of Oz, The (1939)
82	100	3259	4.5	1100186037	Far and Away (1992)
40	100	934	4.5	1100186407	Father of the Bride (1950)
41	100	1028	4.5	1100185898	Mary Poppins (1964)

Now, let’s take a look at which movies we predict userId=100 will like based on their previous ratings. We will need get the row which represents userId=100 and sort their predicted ratings in descending order. np.argsort() is a useful method for getting the top N indices (i.e., movies with highest rating predictions) for userId=100.

top_N = 10

movie_titles = dict(zip(movies['movieId'], movies['title']))

top_N_indices = new_X[user_mapper[userId]].argsort()[-top_N:][::-1]

print(f"Top {top_N} Recommendations for UserId {userId}:")
for i in top_N_indices:
    movie_id = movie_inv_mapper[i]
    print(movie_titles[movie_id])

Top 10 Recommendations for UserId 100:
Forrest Gump (1994)
Pretty Woman (1990)
When Harry Met Sally... (1989)
Apollo 13 (1995)
Toy Story (1995)
Shakespeare in Love (1998)
Aladdin (1992)
Clueless (1995)
Princess Bride, The (1987)
Four Weddings and a Funeral (1994)

Step 8: Evaluation

How do we know if our recommendations are good? The best way to evaluate our system is to test it in the wild with A/B testing or usability tests, where we can get direct feedback from users. However, this option is not always available which means that we need to use offline metrics.

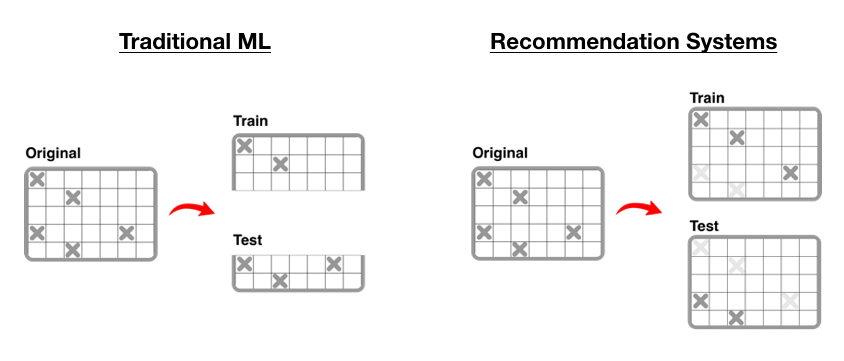
In traditional machine learning, we evaluate a model by splitting our data into two sets: 1) training set and 2) validation set. We train our model using the training set, then test our model on the validation set. In recommender systems, we can’t split our data the traditional way because our model won’t work if our training set represents a completely different user population than the validation set. Instead, we generate our training set by masking random interactions in our user-item matrix. In other words, we pretend that we don’t if a user liked or hated Movie X, but we actually do. Once we train our model and generate our rating predictions, we can then compare our predicted rating with the actual rating.

Image("imgs/splitting.png")

There are various ways to compare our predicted vs. actual ratings. The most common metrics include:

1. Root Mean Squared Error: \(\text{RMSE} = \sqrt{\frac{\Sigma^N_{i=1}(y-\hat{y})^2}{N}}\)
2. Precision: \(\text{Precision} = \frac{TP}{TP+FP}\)
3. Recall: \(\text{Recall} = \frac{TP}{TP+FN}\)